
An Educational Platform for Trading Research
We’re on a mission to make trading knowledge accessible to everyone. We conduct independent research and share our studies to help people learn and grow their understanding of global financial markets.What Kind of Trader Do You Want to Be?
Access our library of quantitative research, including derivatives pricing quizzes, and educational trading strategies.Advanced Mathematics for Trading Research$C = S_0 N(d_1) - K e^{-rT} N(d_2)$
$d_1 = \frac{\ln(S_0 / K) + (r + \frac{\sigma^2}{2})T}{\sigma \sqrt{T}}, \quad d_2 = d_1 - \sigma \sqrt{T}$
// Black-Scholes formula for European call option
double BlackScholesCall(double S, double K, double T, double r, double sigma) {
double d1 = (log(S / K) + (r + 0.5 * sigma * sigma) * T) / (sigma * sqrt(T));
double d2 = d1 - sigma * sqrt(T);
return S * NormalCDF(d1) - K * exp(-r * T) * NormalCDF(d2);
}$C - P = S_0 - K e^{-rT}$
// Put-Call Parity relation
double PutCallParity(double callPrice, double S, double K, double r, double T) {
return callPrice - S + K * exp(-r * T);
}$N(x) = \frac{1}{2} \operatorname{erfc}\left(-\frac{x}{\sqrt{2}}\right)$
// Approximate CDF for the standard normal distribution
double NormalCDF(double x) {
return 0.5 * erfc(-x / sqrt(2));
}Options Pricing Calculator — Live Now!
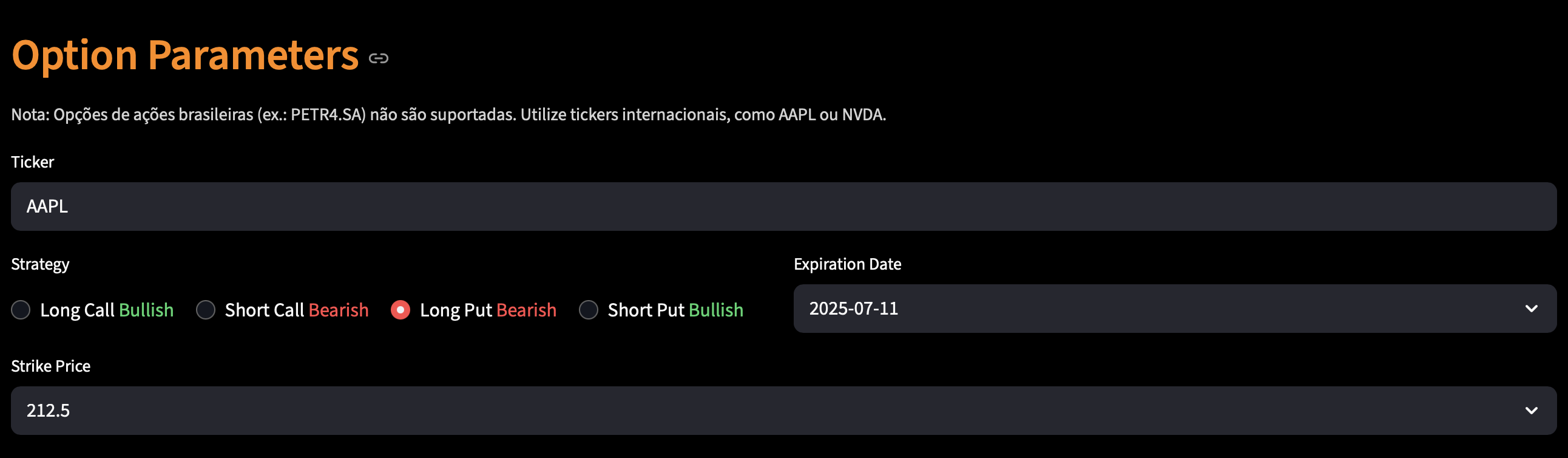
Options Dashboard
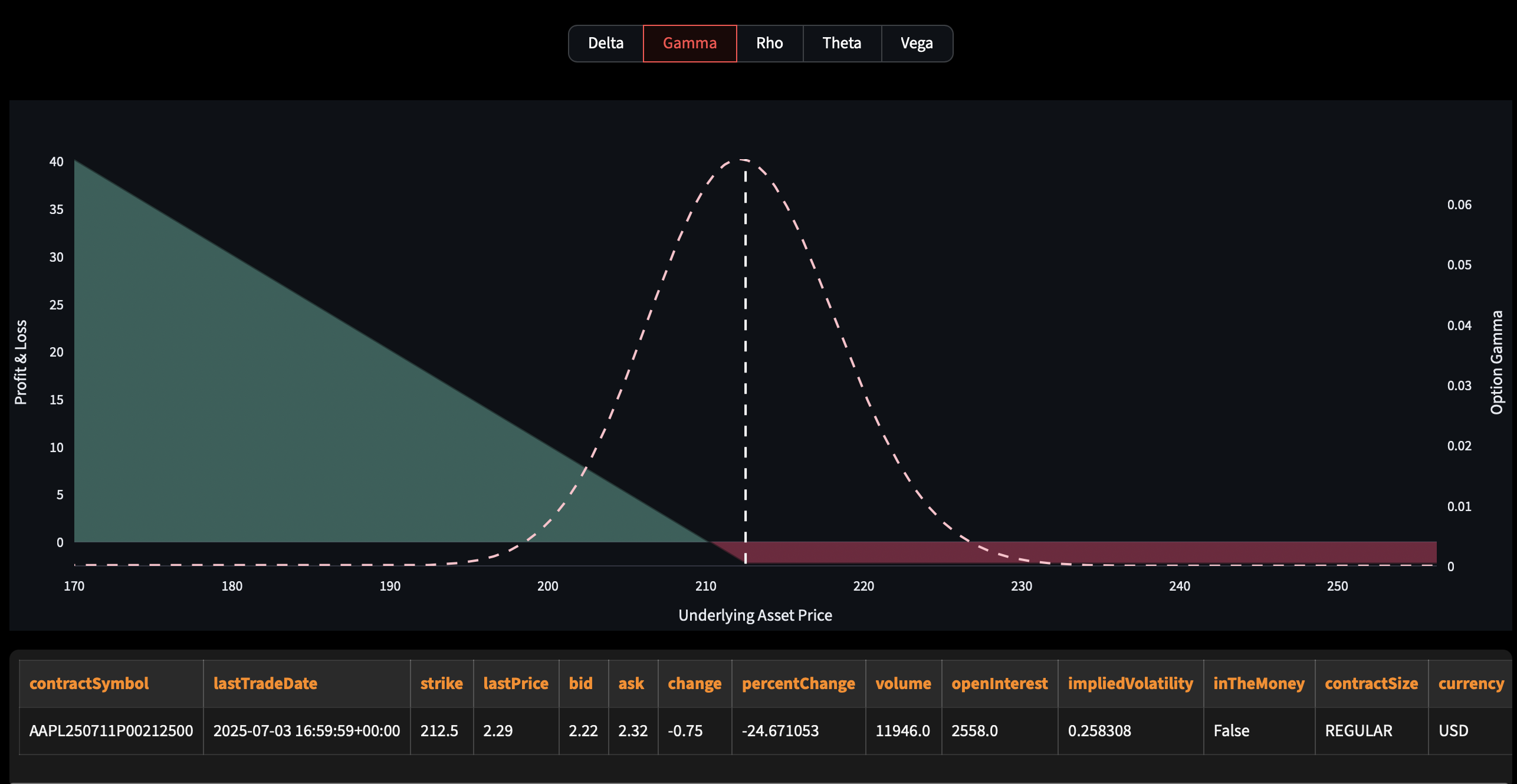
Options Profit & Loss
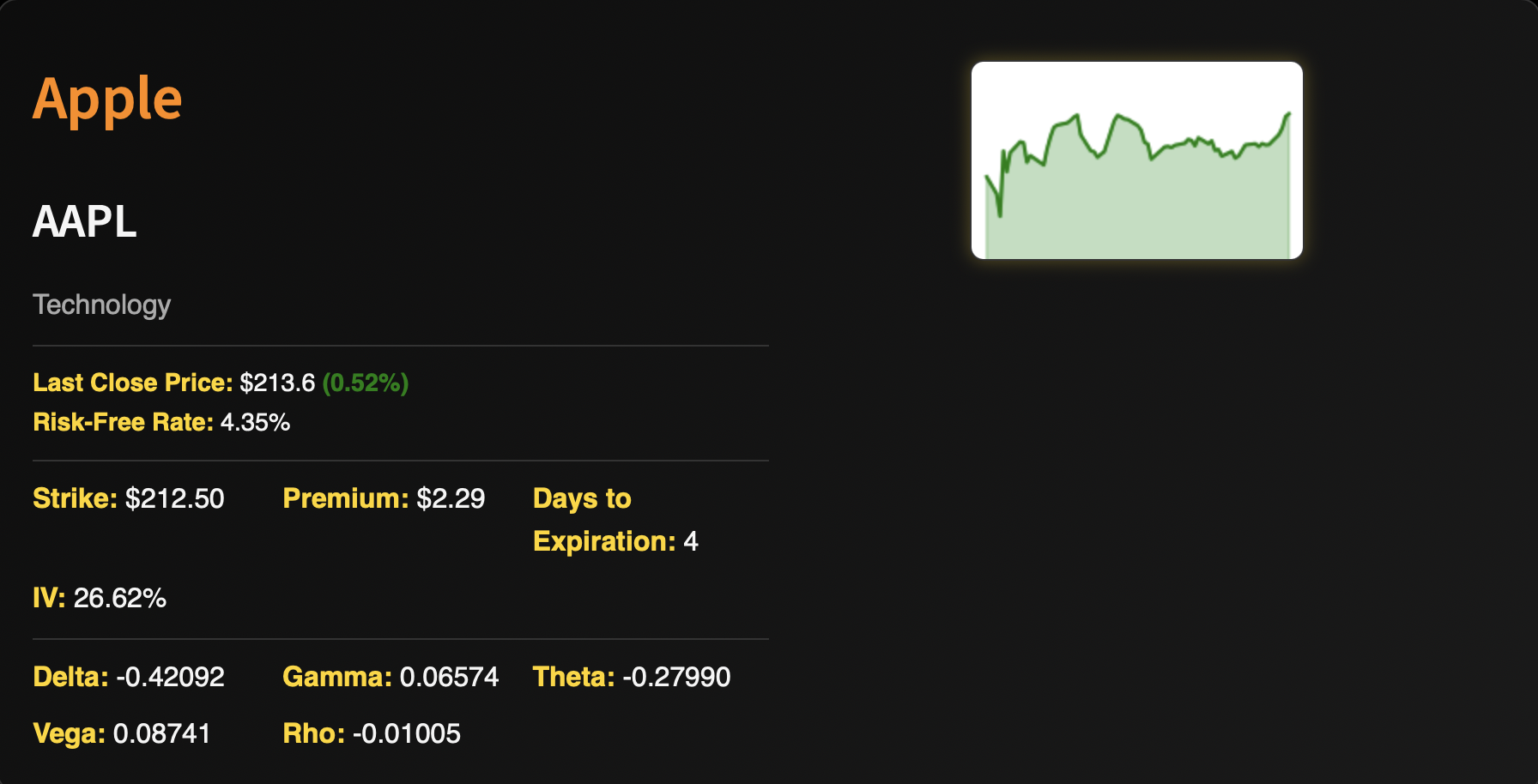
Options Greeks


